1. 数据库系统的结构抽象

1.1 三级模式(三级视图)

  1. External Schema —-（External）View 某一用户能看到与处理的数据的结构描述
  2. (Conceptual) Schema —- Conceptual View 从全局角度理解/管理的数据的结构描述, 含相应的关联约束。体现在数据之间的内在本质联系
  3. Internal Schema —- Internal View 存储在介质上的数据的结构描述，含存储路径、存储方式 、索引方式等

1.2 两层映像

  1. E-C Mapping：External Schema-Conceptual Schema Mapping 将外模式映射为概念模式，从而支持实现数据概念视图向外部视图的转换，便于用户观察和使用
  2. C-I Mapping：Conceptual Schema-Internal Schema Mapping 将概念模式映射为内模式，从而支持实现数据概念视图向内部视图的转换，便于计算机进行存储和处理

1.3 两个独立性

  1. 逻辑数据独立性 当概念模式变化时，可以不改变外部模式(只需改变E-C Mapping)，从而无需 改变应用程序
  2. 物理数据独立性 当内部模式变化时，可以不改变概念模式(只需改变C-I Mapping) ，从而不改 变外部模式

1.4 数据模型

  • 数据模型
    • 规定模式统一描述方式的模型，包括：数据结构、操作和约束
    • 数据模型是对模式本身结构的抽象，模式是对数据本身结构形式的抽象
  • 三大经典数据模型
    • 关系模型：表的形式组织数据
    • 层次模型：树的形式组织数据
    • 网状模型：图的形式组织数据

2. 关系模型的基本概念

2.1 关系模型的三个要素

  1. 基本结构

    形象地说，一个关系(relation)就是一个Table Relation/Table

  2. 基本操作

    基本的

    • 并$\cup$
    • 差：$-$
    • 广义积：$\times$
    • 选择: $\delta$
    • 投影：$\pi$

    扩展的

    • 交: $\cap$
    • 连接: $\Join$
    • 除：$\div$
  3. 完整性约束 实体完整性、参照完整性和用户自定义的完整性

2.2 什么是关系

关系 笛卡尔积中具有某一方面意义的那些元组被称作一个关系

笛卡尔积的数学描述： $$一组域D_1, D_2, … , D_n的笛卡尔积为： D_1 \times D_2 \times \cdots \times D_n = \lbrace (d_1, d_2, \cdots, d_n)| d_i\in D_i,\ i=1, \cdots , n \rbrace$$

2.3 关系模式与关系

  • 同一关系模式下，可有很多的关系
  • 关系模式是关系的结构, 关系是关系模式在某一时刻的数据
  • 关系模式是稳定的；而关系是某一时刻的值，是随时间可能变化的

2.4 关系与表的异同

大部分方面都是相同的，但关系中任意两个元组不能完全相同，而表可能并不完全遵守此特性

2.5 关系的特性

  1. 关系的任意两个元组不能完全相同
  2. 属性不可再分特性:又被称为关系第一范式

2.6 关系上的一些重要概念

候选码/候选键 关系中的一个属性组，其值能唯一标识一个元组，若从该属性组中去掉任何一个属性，它就不具有这一性质了，这样的属性组称作候选码。

主码/主键 当有多个候选码时，可以选定一个作为主码。

主属性和非主属性 包含在任何一个候选码中的属性被称作主属性，而其他属性被称作非主属性

最简单的，候选码只包含一个属性 最极端的，所有属性构成这个关系的候选码，称为全码(All-Key)

外码/外键 关系R中的一个属性组，它不是R的候选码，但它与另一个关系S的候选 码相对应，则称这个属性组为R的外码或外键。

两个关系通常是靠外码连接起来的。

2.3 关系模型的完整性

  1. 实体完整性
    关系的主码中的属性值不能为空值；
    空值：不知道或无意义的值
    意义：关系中的元组对应到现实世界相互之间可区分的一个个个 体，这些个体是通过主码来唯一标识的；若主码为空，则出现不可标识 的个体，这是不容许的

  2. 参照完整性（对外码而言）
    如果关系R1的外码Fk与关系R2的主 码Pk相对应，则R1中的每一个元组的 Fk值或者等于R2 中某个元组的Pk 值， 或者为空值

  3. 用户自定义完整性
    用户针对具体的应用环境定义的完整性约束条件

  • 实体完整性和参照完整性由DBMS系统自动支持
  • DBMS系统通常提供了如下机制：
    • (1)它使用户可以自行定义有关的完整性约束条件
    • (2)当有更新操作发生时，DBMS将自动按照完整性约束条件检验更新操作的正确性，即是否符合用户自定义的完整性

3. 关系代数

3.1 关系代数操作

集合操作和纯关系操作
20210319165048

3.2 关系代数基本操作

3.2.1 关系代数运算的约束

  1. 并相容性
    关系R与关系S存在相容性，当且仅当：
    (1) 关系R和关系S的属性数目必须相同；
    (2) 对于任意i，关系R的第i个属性的域必须和关系S的第i个属性的域相同

3.2.2 关系代数的操作

  1. 并$\vee$(要满足并相容性)
    数学描述： $$R\vee S= \lbrace t|t\in R \vee t \in S \rbrace$$
  2. 差$-$(要满足并相容性)
    数学描述： $$R-S=\lbrace t| t \in R \land t \notin S \rbrace$$
  3. 广义笛卡尔积操作
    数学描述： $$关系R< a_1, a_2, \cdots , a_n>, 关系S<b_1, b_2, \cdots , b_n>, 则 \ R \times S = \lbrace <a_1, a_2, \cdots , a_n, b_1, b_2, \cdots , b_n> | <a_1, a_2, \cdots , a_n> \in R \land <b_1, b_2, \cdots , b_n> \in S \rbrace$$
  4. 选择操作
    数学描述： $$\delta _{con}(R)=\lbrace t | t \in R \land con(t) = true \rbrace$$
  5. 投影
    数学描述： $$\Pi_{a_{i1}, a_{i2}, \cdots, a_{ik}}(R) = \lbrace <t[A_{i1}],t[A_{i2}], \cdots , t[A_{ik}]> | t \in R \rbrace$$ **示例**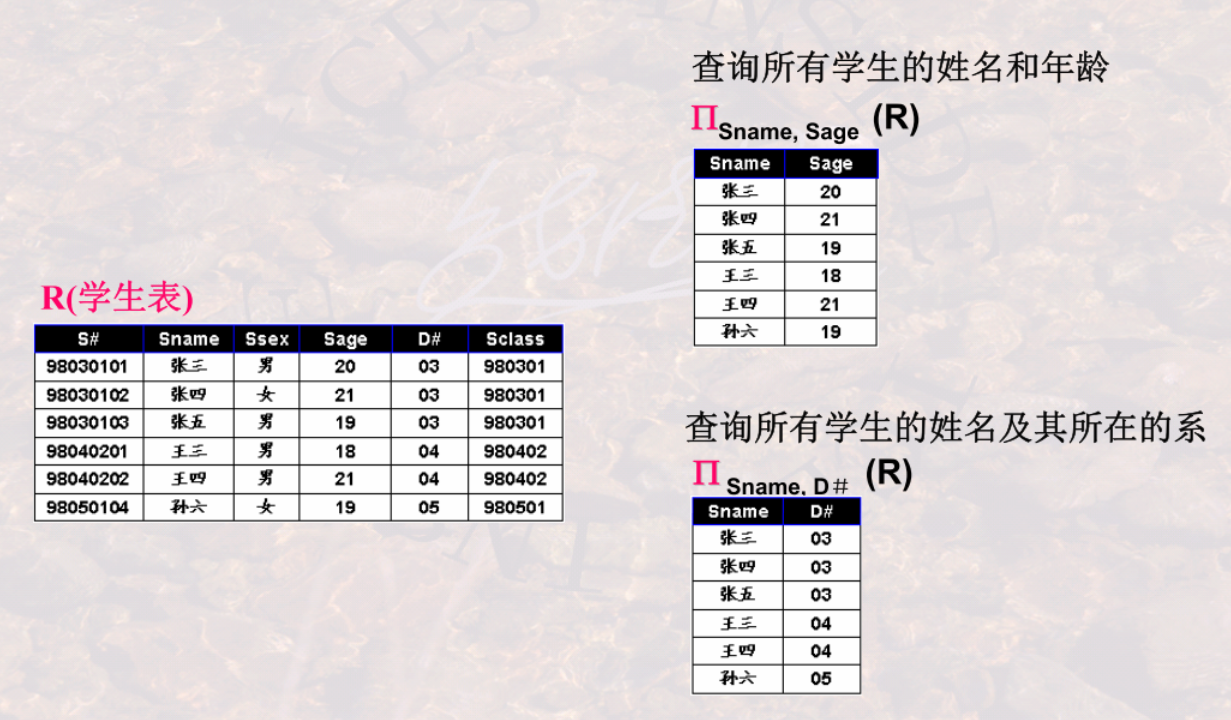
    20210322191913

3.3 关系代数扩展操作

  1. 交
    数学描述：
    $$R \cap S= \lbrace t|t\in R \land t \in S \rbrace$$

  2. $\theta$-连接
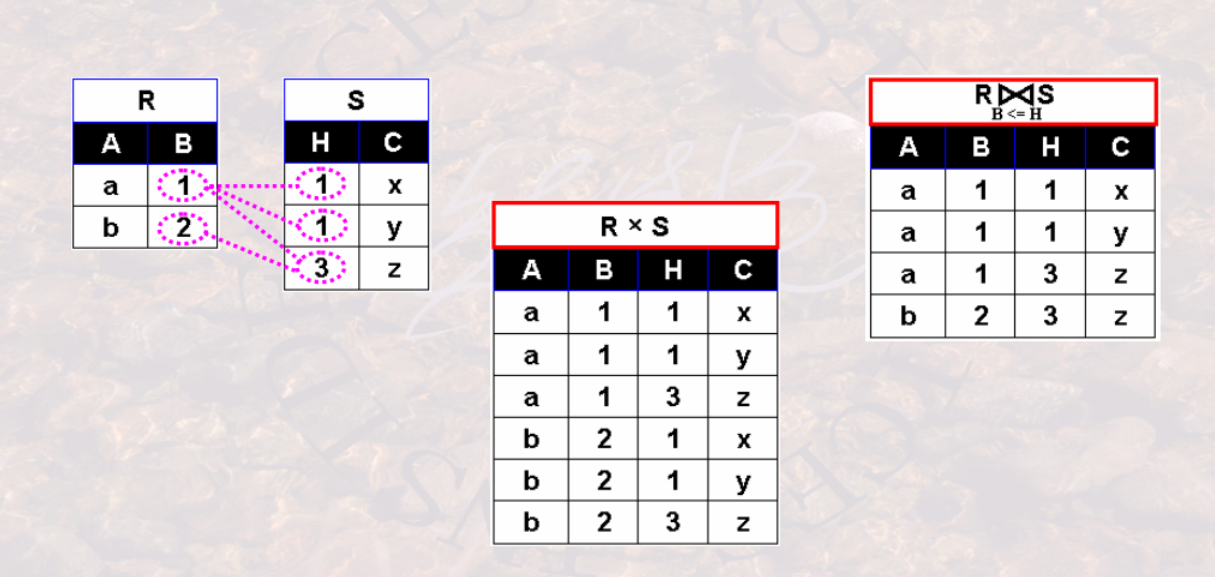
    第一步：对两个表进行广义笛卡尔积
    第二步：从广义笛卡尔积中选取出符合条件的元组
    数学描述： $$R \underset{A \theta B} \Join S = \delta_{t[A] \theta s[B]}(R\times B)$$
    其中$\theta$是比较运算符

    例子

    20210322174239 查询至少98030101号同学和98040202号同学学过的所有课程号
    数学描述： $$\pi_{SC.C}(\delta_{SC.S=“98030101”\land SC1.S=“98040202”}(SC \underset{SC.C=SC1.C} \Join \rho_{SC1} (SC)) $$
    其中$\rho$代表更名操作

  3. 等值连接
    给定关系R和关系S, R与S的等值连接运算结果也是一个关系， 记作$R \underset{A=B} \Join S$，它由关系R和关系S的笛卡尔积中选取R中属性A与S中属性 B上值相等的元组所构成。
    数学描述：
    $$R \underset{A=B}\Join S = \delta_{t[A]=s[B]}(R\times S)$$ 当$\theta$-连接中运算符为“＝”时，就是等值连接，等值连接是$\theta$-连接的一个特例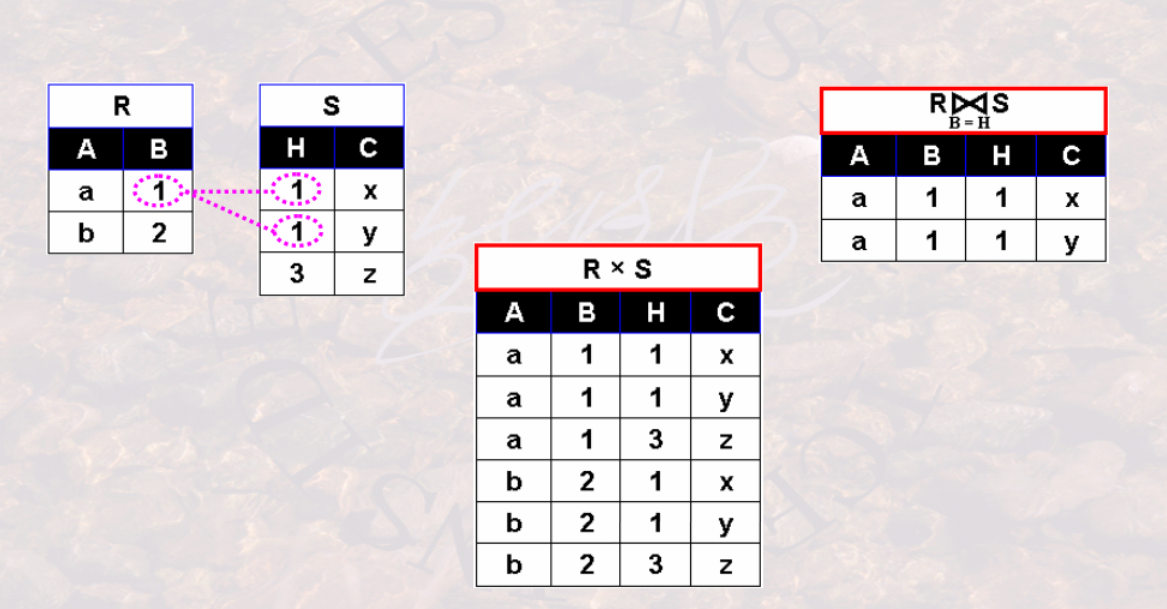； 20210322175401

  4. 自然连接
    给定关系R和关系S, R与S的自然连接运算结果也是一个关系，记作$R \Join S$ ，它由关系R和关系S的笛卡尔积中选取相同属性组B上值相等的元 组所构成。
    数学描述： $$R \Join S = \delta_{t[B]=s[B]}(R\times S)$$
    是一种特殊的等值连接
    要求关系R和S必须有相同的属性组B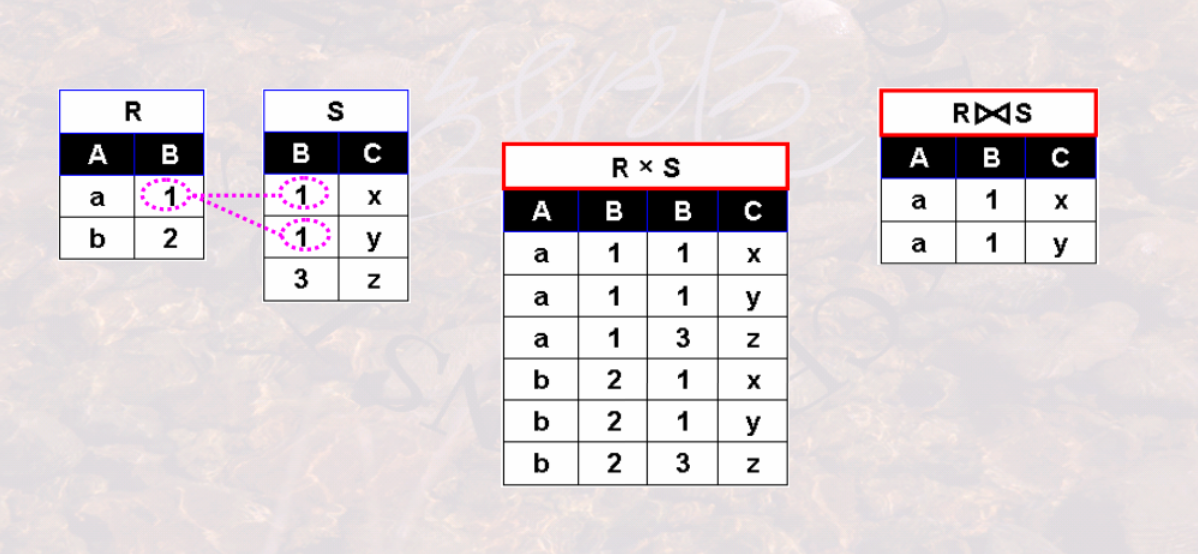
    20210322175636

3.4 关系代数的复杂操作

  1. 除操作$\div$
    前提条件
    若$R(A_1, A_2, \cdots,A_n)$为n度关系，关系$S(B_1, B_2, \cdots, B_n)$为m度关系，只有当$\lbrace B_1, B_2, \cdots, B_n\rbrace \subseteq \lbrace A_1, A_2, \cdots,A_n \rbrace $即B是A的真子集，$m<n$时才可进行$R\div S$运算
    定义
    设关系$R<a_1, \cdots, a_n>$和关系$S<b_1, \cdots, b_m>$,那么$R\div S$结果为关系为元组$<c_1, \cdots, c_k>$的集合，元组$<c_1, \cdots, c_k>$满足下述条件:它与S中每一个元组$<b_1, \cdots, b_m>$组合形成的一个新元组都是R中的某一个元组$<a_1, \cdots, a_n>$
    示例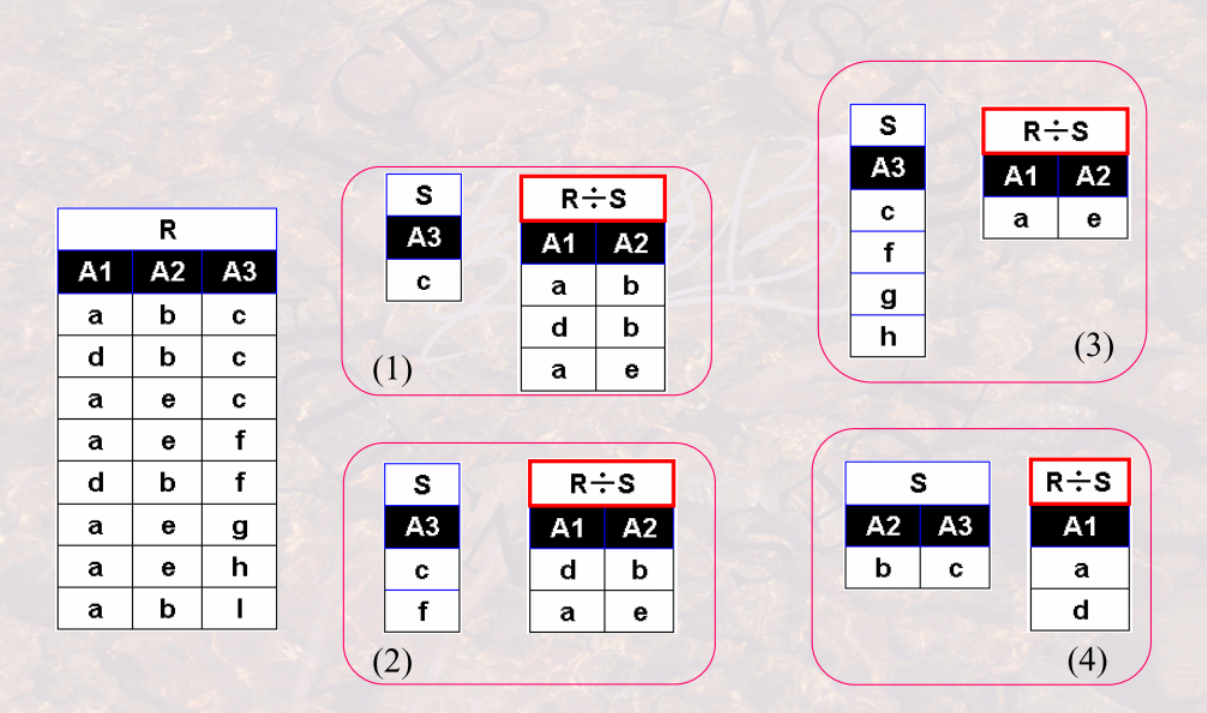 20210322191642

    1. 外连接（Outer-Join）
      定义
      两个关系R与S进行连接时，如果关系R(或S)中的元组在S(或R)中找不到相匹配的元组，则为了避免该元组信息丢失，从而将该元组与S(或R)中 假定存在的全为空值的元组形成连接，放置在结果关系中，这种连接称之为外连接(Outer Join)。
      外连接 = 自然连接 (或$\theta$连接) + 失配的元组(与全空元组形成的连接)
      外连接的形式
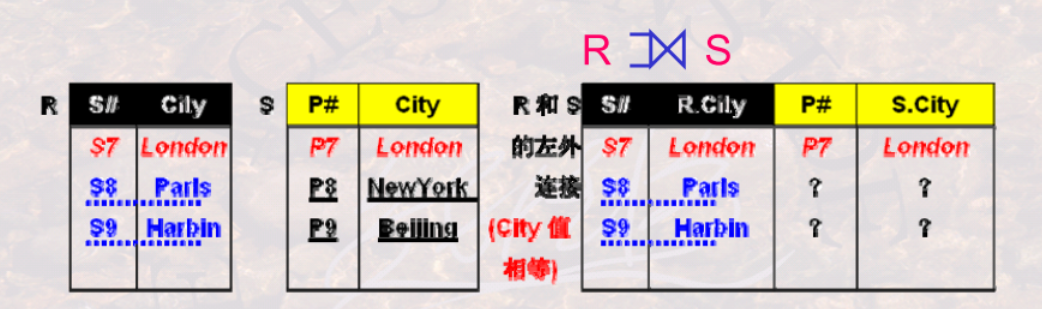
    • 左外连接 = 自然连接(或$\theta$连接) + 左侧表中失配的元组。 记作$⟕$ 20210322192639
    • 右外连接 = 自然连接(或$\theta$连接) + 右侧表中失配的元组。 记作 $⟖$
      20210322192701
    • 全外连接 = 自然连接(或$\theta$连接) + 两侧表中失配的元组。 记作$⟗$
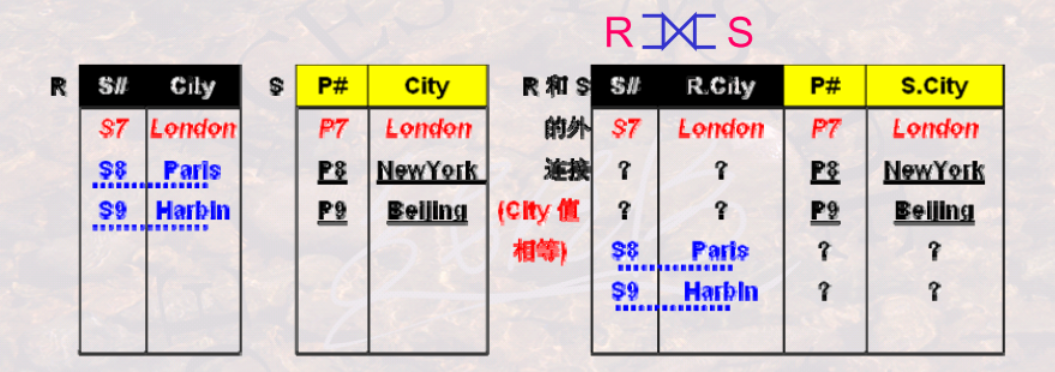
      20210322192739

4. 关系演算

  1. 关系元组演算

    以元组变量作为谓词变量的基本对象

  2. 关系域演算

    以域变量作为谓词变量的基本对象

4.1 关系元组演算

基本形式
$$\lbrace t | P(t)\rbrace$$
其中，$P(t)$可以是如下三种形式之一的原子公式：

  • $t\in R$
  • $s[A] \theta c$
    其中$\theta$为比较运算符$<, \le, \ge, >, \ne$
    例如$\lbrace t| t\in R \land t[Sage]\le 19 \land t[Sname] = ‘Bob’\rbrace$
  • $s[A] \theta u[B]$
    s[A]与u[B]为元组分量，A和B分别是某些关系的属性，他们之间满足比较关系$\theta$
    例如：检索除年龄不是最小的所有同学
    $\lbrace t|t\in Student \land \exist (u \in Student)(t[Sage]>u[Sage])\rbrace$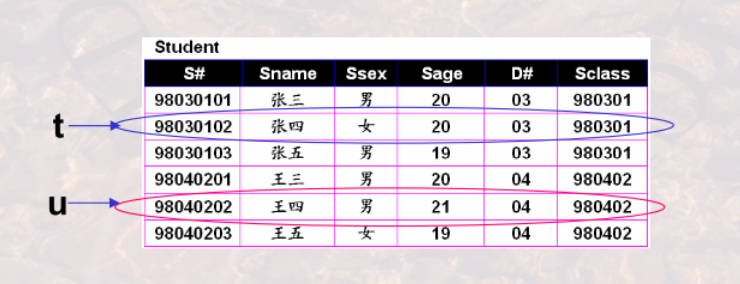
    20210323102115

4.2 关系域演算

…

关系数据库中的范式

  1. 第一范式（1NF）
    关系的每一个分量都是不可分的数据项
  2. 第二范式（2NF）
    若$R\in 1NF$,且每一个非主属性完全函数依赖于任何一个候选码，则$R\in 2NF$
  3. 第三范式（3NF）
    设关系模式$R<U,F>\in 1NF$, 若R中不存在这样的码X，属性组Y及非主属性$Z(Z\nsubseteq Y)$，使得$X\rightarrow Y, Y \rightarrow Z$成立，$Y\nrightarrow X$, 则称$R<U,F>\in 3NF$。用人话说就是，若$R\in 3NF$,则每一个非主属性既不传递依赖于码，也不部分依赖于码。
  4. BC范式 关系模式$R<U,F>\in1NF$,若$X\rightarrow Y$且$Y\nsubseteq X$时必含有码，则$R<U,F>\in BCNF$。也就是说，关系模式$R<U,F>$中，若每一个决定因素都包含码，则$R<U,F>\in BCNF$
    一个满足BCNF的关系模式有：
    • 所有非主属性对每一个码都是完全函数依赖
    • 所有主属性对每一个不包含它的码也是完全函数依赖
    • 没有任何属性完全函数依赖于非码的任何一组属性